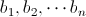Finite Dimensional Linear Algebra: I learned Linear Algebra by this book.
Linear Algebra Done Right: My professor who taught vector space when I was freshman recommended to read this book.
I already know
linearly independent: http://sailingkyle.blogspot.com/2011/08/mathlinear-algebra-linearly-independent.html
and span: http://sailingkyle.blogspot.com/2011/08/mathlinear-algebra-span.html
Then now I ready for define basis.
Definition of basis
Let V be a vector space over V. For { } ⊆V, if {
} ⊆V, if { } is
} is
LINEARLY INDEPENDENT and SPANS V,
then we call{ } is a BASIS for V.
} is a BASIS for V.
Basis can be defined by other ways. Here is another definition.
Alternative definition of basis
If for∀v∈V, if v can be written as a LINEAR COMBINATION
of UNIQUELY,then we call{
UNIQUELY,then we call{ } is a BASIS for V.
} is a BASIS for V.
Proof for equivalence.
For each v∈V, if v= for unique
for unique  .
.
∴{ } spans V.
} spans V.
The solution of =0 is unique since 0 can be written as a linear combination of
=0 is unique since 0 can be written as a linear combination of uniquely.
uniquely.
Trivial solution of it is and it is a unique solution.
and it is a unique solution.
∴{ }is linearly independent. Q.E.D.
}is linearly independent. Q.E.D.
Here is a example of basis for a vector space which called a standard basis.
which called a standard basis.
Def)  i th element is 1, others are all zero.
i th element is 1, others are all zero. ∈
∈ ,
,
For example, ∈
∈ is (1,0,0) and
is (1,0,0) and  ∈
∈ is (0,0,1)
is (0,0,1)
We call { } is a standard basis. for
} is a standard basis. for 
proof for { } is a basis for
} is a basis for 
i)Linearly independent
If =0, then =0
=0
∴
∴{ } is linearly independent
} is linearly independent
ii) Span
For any ∈
∈ , ∃
, ∃ such that
such that
 =
=
∴{ } spans
} spans 
∴{ } is linearly independent and spans
} is linearly independent and spans  so it is a basis for
so it is a basis for  .
.
Linear Algebra Done Right: My professor who taught vector space when I was freshman recommended to read this book.
I already know
linearly independent: http://sailingkyle.blogspot.com/2011/08/mathlinear-algebra-linearly-independent.html
and span: http://sailingkyle.blogspot.com/2011/08/mathlinear-algebra-span.html
Then now I ready for define basis.
Definition of basis
Let V be a vector space over V. For {
 } ⊆V, if {
} ⊆V, if { } is
} isLINEARLY INDEPENDENT and SPANS V,
then we call{
 } is a BASIS for V.
} is a BASIS for V.Basis can be defined by other ways. Here is another definition.
Alternative definition of basis
If for∀v∈V, if v can be written as a LINEAR COMBINATION
of
 UNIQUELY,then we call{
UNIQUELY,then we call{ } is a BASIS for V.
} is a BASIS for V.Proof for equivalence.
 for unique
for unique  .
.∴{
 } spans V.
} spans V.The solution of
 =0 is unique since 0 can be written as a linear combination of
=0 is unique since 0 can be written as a linear combination of uniquely.
uniquely.Trivial solution of it is
 and it is a unique solution.
and it is a unique solution.∴{
 }is linearly independent. Q.E.D.
}is linearly independent. Q.E.D.Here is a example of basis for a vector space
 which called a standard basis.
which called a standard basis. i th element is 1, others are all zero.
i th element is 1, others are all zero. ∈
∈ ,
,For example,
 ∈
∈ is (1,0,0) and
is (1,0,0) and  ∈
∈ is (0,0,1)
is (0,0,1) } is a standard basis. for
} is a standard basis. for 
proof for {
 } is a basis for
} is a basis for 
i)Linearly independent
 =0
=0∴

∴{
 } is linearly independent
} is linearly independentii) Span
For any
 ∈
∈ , ∃
, ∃ such that
such that =
=
∴{
 } spans
} spans 
∴{
 } is linearly independent and spans
} is linearly independent and spans  so it is a basis for
so it is a basis for  .
.