Finite Dimensional Linear Algebra: I learned Linear Algebra by this book.
Linear Algebra Done Right: My professor who taught vector space when I was freshman recommended to read this book.
Both linearly independent and span are important for define basis, a useful concept of linear algebra.
We defined span in previous post, see: http://sailingkyle.blogspot.com/2011/08/mathlinear-algebra-span.html
Here is definition of linearly independent.
we say it is linearly dependent.
For a, b,c∈F, if a(1,0,0)+b(0,1,0)+c (0,1,1)=0,
(a,b+c,c)=0
∴ a=c=b=0
∴ {(1,0,0), (0,1,0), (0,1,1) } is linearly independent.
Here is a useful theorem.
 ≠ 0.
≠ 0.k≥2 since if k=1,
 , which means it is linearly independent.
, which means it is linearly independent.Then
 is a linear combination of other vectors. Done.
is a linear combination of other vectors. Done.<=)if
 ≠ 0 can be written as other vectors,
≠ 0 can be written as other vectors,






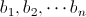
No comments:
Post a Comment